

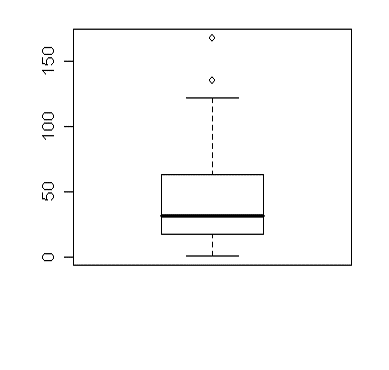
The larger median, the larger the average. The median is found at the position of the line inside the box. The lower and upper quartiles are located at the upper and lower edges of the box portion of the plot. The minimum and maximum are located at the ‘whiskers’ of the plot. Read the median which is in line with the line inside the box.Ī box plot is also known as a box and whisker plot.Read the upper quartile which is in line with the end of the box.Read the lower quartile which is in line with the start of the box.Read the maximum value in line with the last line.Read the minimum value in line with the first line.
Two box plots same graph r how to#
How to Read a Box Plot To read a box plot: Side-by-side box plots allow for two or more data sets to be compared in a graphical form. From this, the spread and skew of the data can also be seen. The distribution of data is shown through the positions of the median and the quartiles. In statistics, a box plot is used to provide a visual summary of data. Box plots are a useful way to compare two or more sets of data visually.

From this, the range, interquartile range and skewness of the data can be observed. A box plot indicates the position of the minimum, maximum and median values along with the position of the lower and upper quartiles.
Two box plots same graph r code#
This uses code coming from jbburant and David Robinson.A box plot is a diagram used to display the distribution of data. Thus, a good alternative is a half violin plot showing the raw data. However, it is sometimes better to show the data points themselves. This is a good practice and shows that group C is under-represented. On the previous chart, the sample size of each group is indicated on the x-axis, below the group name. Violin plots are a powerful way to display information–they are probably under-utilized compared to boxplots.
The bimodal distribution of group B becomes obvious. Here it is very clear that the groups have different distributions. ) + ggtitle( "A boxplot with jitter") + xlab( "") Sample_size = data %>% group_by(name) %>% summarize( num= n())ĭata %>% left_join(sample_size) %>% mutate( myaxis = paste0(name, " \n ", "n=", num)) %>% ggplot( aes( x=myaxis, y=value, fill=name)) + geom_violin( width= 1.4) + geom_boxplot( width= 0.1, color= "grey", alpha= 0.2) + scale_fill_viridis( discrete = TRUE) + theme_ipsum() + theme( However, we cannot see the underlying distribution of dots in each group or their number of observations. If we consider the boxplot below, it is easy to conclude that group C has a higher value than the others. The problem is that summarizing also means losing information, and that can be a pitfall. Here is a diagram showing the boxplot anatomy:Ī boxplot can summarize the distribution of a numeric variable for several groups. Dots (or other markers) beyond the extreme line shows potntial outliers.



 0 kommentar(er)
0 kommentar(er)
